O que é Lógica?
Você sabe o que é Lógica? A lógica é uma palavra de origem grega que vem de “Logos”, a determinação tem várias possibilidades de tradução: palavra, pensamento, razão ou até mesmo raciocínio.
A lógica é o estudo da arte de argumentar, ou seja, a construção do argumento, base essa para um discurso coerente. As principais regras da lógica foram criadas por ninguém mais e ninguém menos que Aristóteles, o filósofo criou as regras no século IV a.C.
Vamos aprender um pouco mais?
O que é Lógica? LÓGICA FILOSÓFICA
A lógica pode ser entendida como uma sequência de fatos ocorridos, ou seja, podemos entendê-la como uma organização primeira, essa lógica primária é construída através de uma técnica e/ou de uma ciência, temos como exemplo a lógica matemática, lógica computacional, e não podemos esquecer-nos da mais falada e complexa de todas, a lógica filosófica.
A lógica filosófica é uma temática muito importante dentro da filosofia, ramo esse que busca respaldar o chamado passo a passo do raciocínio, do pensamento em suas determinantes, como exemplo a argumentação, e a partir da argumentação pode ser construído a forma de pensar.
Além do mais, a lógica estuda alguns meios de raciocínio considerados importantes no meio do conhecimento, como raciocínio dedutivo, indutivo e abdutivo, mas pensa que acabou? Não! Pois a lógica dentro da filosofia é muito ampla, além de estudar essas variáveis, também se utiliza de recursos linguísticos, como a argumentação, já mencionada, e as inferências lógicas.
TIPOS DE RACIOCÍNIO LÓGICO
A lógica dentro da filosofia aborda três tipos de raciocínio dedutivo, indutivo e abdutivo, além de interligar outros dois, que são a inferência e o argumento, vamos conhecer cada um deles?
Dedutivo: A dedução nada mais é o raciocínio que irá determinar uma conclusão, ou seja, um resultado, esse resultado vem a partir de premissas, premissas essas que são pontos ou ideias a qual surge um raciocínio lógico. A premissa é considerada uma teoria geral, já a segunda será um caso particular, individual, sobre aquilo que está sendo levantado, falado, a partir da teoria geral e do caso particular irá dar o resultado de uma conclusão válida.
EXEMPLO: (Se A é B e B é C) conclui-se a partir disso logicamente que C é igual a A, ou seja, três elementos que se conectam entre si e trás uma lógica pura, a relação de igualdade entre o C e o A.
Outro exemplo bastante utilizado é o silogismo:
Todo homem é mortal. (Premissa 1)
João é homem. (Premissa 2)
Logo, João é mortal. (Conclusão)
A partir dessa premissa há uma teoria geral e através disso se pega um caso particular, como João. O raciocínio dedutivo pode ser muito encontrado e pensado no trabalho do matemático, sim, o matemático utiliza de conclusões, essas conclusões são encontradas a partir de premissas e teorias gerais, essas teorias são mostradas em somas e através dessa soma há resultados, esses resultados advêm a partir de teorias gerais encontradas sobre algarismo.
Indutivo: Diferentemente do método dedutivo, o indutivo não busca conclusões, resultados, e sim através de premissas determinam as teorias e as regras gerais de casos particulares. As ciências da natureza (física, química, biologia) trabalham mais esse método, pois há uma busca de dados na natureza e no mundo empírico colhendo informações, através dessa busca os profissionais podem observar certa repetição de dados, ou seja, com isso induzem que os fatos coletados são definidos como regra geral.
EXEMPLO: Todas as maças têm sementes, essa descoberta veio através de uma análise realizada na fruta, e a partir dessa análise e de outras maças, percebe-se que em todas há presença de sementes, a partir disso é induzido que há uma regra geral e que todas ou quase todas as maças tem sementes.
Abdução: O método é considerado o mais complexo dentre os outros métodos mencionados, a abdução além de determinar uma conclusão a partir de um raciocínio, e também induzir uma regra geral, busca através dessa junção a experiência desses fatores, ou seja, o saber ouvir, o olhar, a conexão dos fatos a partir de teorias e através disso determina as premissas. A abdução pode ser usada como exemplo no trabalho do policial, detetive, médico, entre outros.
Ex: O paciente chega ao hospital apresentando diversos sintomas, como tais: febre, dor de cabeça, náuseas, sintomas esses conclusivos trazidos pelo paciente, o médico avalia esses sintomas através do olhar, do saber ouvir, e a partir dos sintomas conclusivos, faz exames, os exames pode ser entendidos como “investigativo”, investigar empiricamente, e conectar os dados de conhecimento com teorias, regras gerais a partir de um caso particular.
Inferência: É o ato de inferir sobre uma preposição:
Exemplo:
Todos precisam se alimentar (1 preposição)
João gosta da hora do almoço (2 preposição)
A partir disso é entendido que há uma relação direta daquilo que foi dito e aquilo que foi proposto, com outra preposição, a partir disso é tirado uma conclusão. A inferência é usada quando é determinada uma verdade ou a falsidade daquilo que está sendo exposto.
Argumento: O argumento é considerado um tipo de raciocínio dentro de um procedimento lógico, o mesmo é utilizado para defender pensamentos, ideias, opiniões e desenvolvimento de defesas.
O argumento pode apresentar duas formas: Válida ou inválida, um exemplo disso é: Todo homem é mortal, Sócrates é homem, portanto Sócrates é mortal, nessa frase representa bem um silogismo válido, ou seja, há uma conexão lógica válida, como mesmo já vista.
Mas há lógicas válidas que podem ser consideradas inválidas quando não apresentam uma verdade mundial entre os dois fatores: Ex: Charles Bukowsk foi o primeiro homem a pisar na lua, ou seja, há uma forma válida, lógica, mas não corresponde uma verdade no mundo, pois Charles foi um grande poeta da Alemanha, e quem pisou na lua foi Neil Armstrong.
Quando o argumento não passa por uma lógica bem construída é chamado de argumento falacioso.
A falácia dentro do argumento são formas inválidas, não há lógica bem construída, mas é preciso entender que falácia não é sinônimo de mentira, a mentira é um tipo de falácia, mas falácia são argumentos inválidos que podem levar ao engano. Há inúmeros tipos, como o equívoco, ênfase, apelo a força, apelo a emoção, falsa causa, inversão de causa e efeito entre outros.
LÓGICA SIMBÓLICA
Na lógica simbólica, também denominada de lógica formal, diferentemente do raciocínio lógico, há a redução das proposições, ou seja, o que é falado, argumentado, não é tão mais importante no conceito simbólico, e sim na forma.
Os símbolos são representados em tabelas, chamadas de “tabelas da verdade”, com proposições em letras: p, qe r. No campo da lógica formal é colocado a relação entre as preposições com os chamados operadores lógicos, que são eles: conjunções, disjunções e condicionantes.
LÓGICA PROPOSICIONAL
A lógica proposicional estuda as preposições que podem ser representadas por diversos elementos, esses elementos são as bases para a validação de um determinado enunciado.
Há uma junção lógica entre as preposições e a partir disso torna-se possível o encadeamento lógico das estruturas, vejamos alguns exemplos:
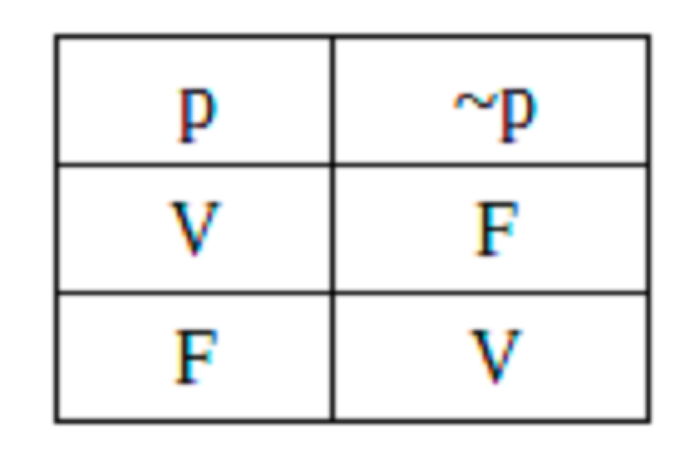
Negação: A negação é quando há uma sentença, e nessa sentença há uma negação de um termo representado pelo símbolo ~ ou ¬ , ou seja, a negação de “P” é ~ p ou ¬ p. Na tabela a negação de “P” é igual ¬ p. Se “ P” é verdadeiro, ¬ p é falso, e vice-versa
Para entendermos melhor, a letra P dentro da sentença é verdadeira ou podemos negá-la e dizer que é falsa. Exemplo: (Está nevando = P verdadeiro) negação dessa frase (não está nevando = P falso) ou vice versa.
Esta é a tabela que representa a teoria acima.
Conjunção (∧): Na língua portuguesa a conjunção é representa pela letra “e”, dentro da lógica proposicional é representa por esse símbolo (∧). Toda vez que tiver uma sentença com conjunção significa que todos os elementos do conjunto devem acontecer simultaneamente para que assim a sentença se torne verdadeira. Exemplo:
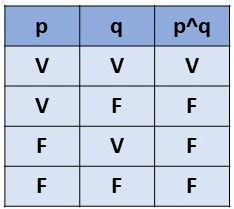
Como a tabela mesmo mostra para a sentença ser verdadeira p e q precisam estar juntos, portando se é verdadeiro p e é verdadeiro q, a sentença final é verdadeira, mas, se p é verdadeiro e q é falso, a sentença final é falsa e vice versa, e se p e q forem sentenças falsas, consequentemente a sentença final também será falsa.
Disjunção (V): Na língua portuguesa o símbolo equivale à conjunção alternativa “ou”. Somente será falsa se ambos os termos forem falsos. Pensamento esse logicamente diferente da conjunção, a sentença não precisa acontecer simultaneamente, mais sim um ou outro. Vejamos o exemplo na tabela:
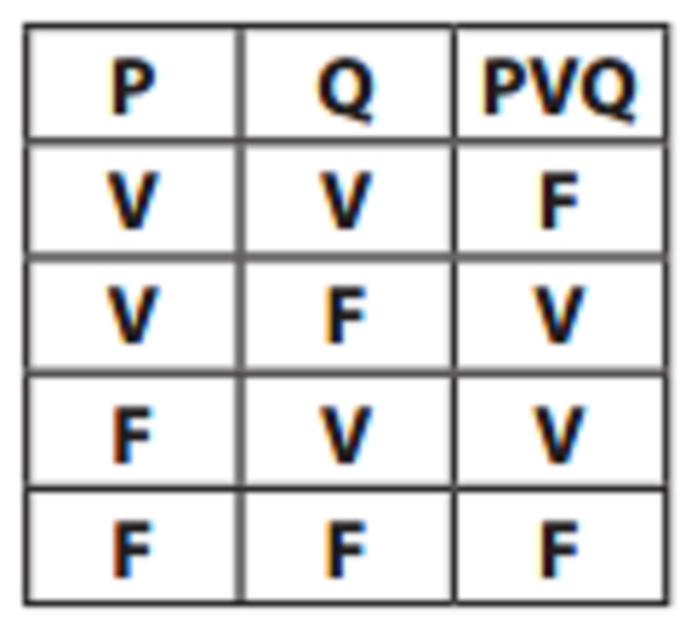
Se formos analisar a tabela para que sentença final PVQ possa ser falsa, as duas sentenças p e q têm que ser obrigatoriamente falsas, ou seja, a sentença final falsa só acontece quando o p e q sucedem de formas iguais (F, F, V, V)
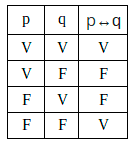
Condicional (→): Condicional é algo que implica condição, precisa acontecer algo para acontecer outro algo: O necessário chamamos de (Q) o suficiente (P). Acontece o suficiente para assim acontecer o necessário. Na língua portuguesa podemos pensar esse contexto na condicionante “se” ou “então” Ex: Se está chovendo, então as plantas estão molhadas.
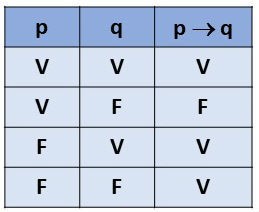
Se o suficiente (p) e o necessário (q) são verdadeiros, a preposição final será verdadeira, se o (p) suficiente ser falso, enquanto o necessário (q) é verdadeiro, a preposição será verdadeira, se acontece ao contrario, o suficiente ser verdadeiro e o necessário ser falso, a preposição será falsa, mas se eu tenho (p) e (q) falsos, a sentença será verdadeira, isso pode ser entendido através de uma equação matemática onde dois sinais negativos são positivos no final.
Bicondicional (⇔): Por fim a Bicondicional é formada por duas condicionais, só será falsa se as preposições tiverem individualmente valores diferentes.
As tabelas de verdade são utilizadas na lógica para orientar e determinar se as fórmulas lógicas determinadas por sentenças são válidas ou inválidas, mas por muitos são consideradas bem complexas de serem entendidas.
Conteúdo original, não se esqueça de referenciar: Disponível em: <https:/filosofia/o-que-e-logica/>
Outros artigos recomendados:









